순열
재귀를 사용한 순열
O(n!)
public class Main {
static char[] src = {'a', 'b', 'c', 'd'};
public static void main(String[] args) {
// 4P3
makePermutation(0, new char[3], new boolean[src.length]);
}
static void makePermutation(final int nthChoice, char[] choosed, boolean[] visited) {
// 기저 조건
if(nthChoice == choosed.length) {
System.out.println(Arrays.toString(choosed));
return;
}
// 재귀처리
for (int i = 0; i < src.length; i++) {
if(!visited[i]) {
visited[i] = true;
choosed[nthChoice] = src[i];
makePermutation(nthChoice + 1, choosed, visited);
visited[i] = false;
}
}
}
}
Java
복사
이미 사용한 원소를 재사용할 수 없으므로 visited 배열로 사용여부를 확인해주어야함.
중복 순열
public class Main {
static char[] src = {'a', 'b', 'c', 'd'};
public static void main(String[] args) {
makeDupPermutation(0, new char[3]);
}
static void makeDupPermutation(final int nthChoice, char[] choosed) {
// 기저 조건
if(nthChoice == choosed.length) {
System.out.println(Arrays.toString(choosed));
return;
}
// 재귀 처리
for (int i = 0; i < choosed.length; i++) {
choosed[nthChoice] = src[i];
makeDupPermutation(nthChoice + 1, choosed);
}
}
}
Java
복사
기존 순열에서 중복이 허용되므로 visited 배열을 사용하지 않음
조합
O(2^n)
public class Main {
static char[] src = {'a', 'b', 'c', 'd'};
public static void main(String[] args) {
makeCombination(0, 0, new char[3]);
}
static void makeCombination(final int nth, final int startIdx, char[] choosed) {
if(nth == choosed.length) {
System.out.println(Arrays.toString(choosed));
return;
}
for (int i = startIdx; i < src.length; i++) {
choosed[nth] = src[i];
makeCombination(nth + 1, i + 1, choosed);
}
}
}
Java
복사
순열과 달리 순서가 중요하지 않음. [1, 2] = [2, 1]
→ 결과가 중복되는 것을 방지하기 위해 현재 선택한 원소보다 뒤에 있는 원소에 대해서만 탐색을 진행한다
파스칼의 삼각형을 사용하면
중복 조합
public class Main {
static char[] src = {'a', 'b', 'c', 'd'};
public static void main(String[] args) {
makeDupCombination(0, 0, new char[3]);
}
static void makeDupCombination(final int nth, final int startIdx, char[] choosed) {
if(nth == choosed.length) {
System.out.println(Arrays.toString(choosed));
return;
}
for (int i = startIdx; i < src.length; i++) {
choosed[nth] = src[i];
makeDupCombination(nth + 1, i, choosed);
}
}
}
Java
복사
조합과 달리 중복이 가능하다,
따라서 현재 선택한 원소보다 뒤에 있는 원소에 대해서만 탐색을 진행했던 것과 달리, 현재 선택한 원소도 포함하여 탐색을 진행
부분집합
public class Main {
static char[] src = {'a', 'b', 'c', 'd'};
public static void main(String[] args) {
makeSubSet(0, new boolean[4]);
}
static void makeSubSet(final int nthCheck, boolean[] status) {
if(nthCheck == status.length) {
printSubSet(status);
return;
}
status[nthCheck] = true;
makeSubSet(nthCheck + 1, status);
status[nthCheck] = false;
makeSubSet(nthCheck + 1,status);
}
private static void printSubSet(boolean[] status) {
System.out.print("[");
for(int i = 0; i < status.length; i++) {
if(status[i]) {
System.out.print(src[i]);
}
}
System.out.println("]");
}
}
Java
복사
부분집합은 해당 원소를 사용했느냐 안했느냐의 여부만 판단하면 된다.
따라서 boolean 배열을 통해 해당 index의 원소를 사용했는지 체크해준다.
private static void makeSubSet2() {
for (int i = 0; i < 1 << src.length; i++) {
System.out.print("[");
for (int j = 0; j < src.length; j++) {
if((i & (1 << j) ) > 0) {
System.out.print(src[j]);
}
}
System.out.println("]");
}
}
Java
복사
NextPermutation
O(n)
nPn 의 순열을 구할 때 사용함
기존 순열 찾는 코드와 달리 더 빠른 속도 보장!
// nextPermutation -> 순열 중 빠르지만 nPn을 다 구할 때 사용
private static boolean nextPermutation() {
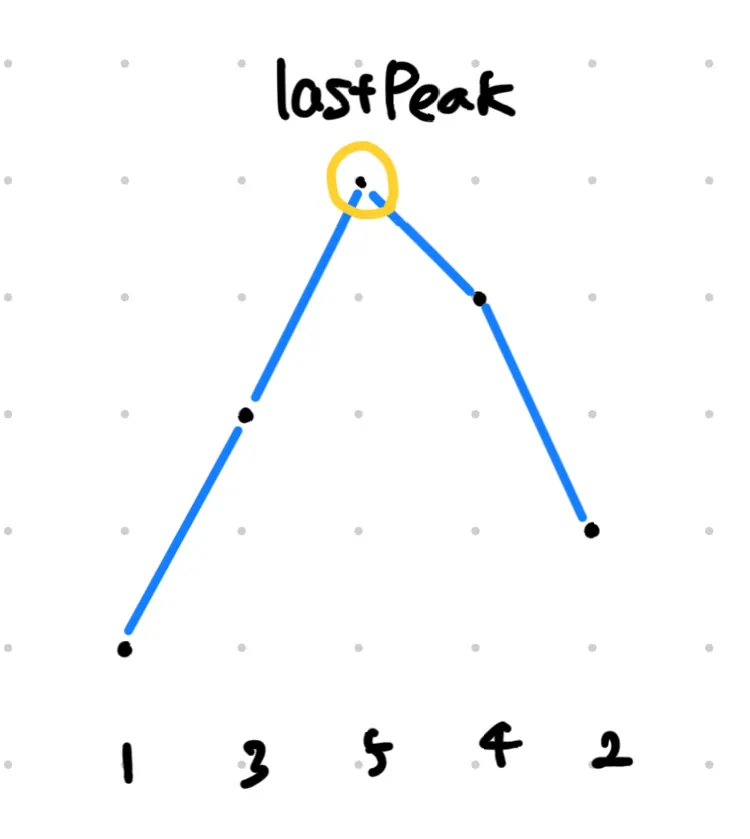
// 1. 최고 정점 찾기
int lastPeak = src.length - 1;
while(lastPeak > 0 && src[lastPeak - 1] >= src[lastPeak]) lastPeak--;
if(lastPeak == 0) return false;
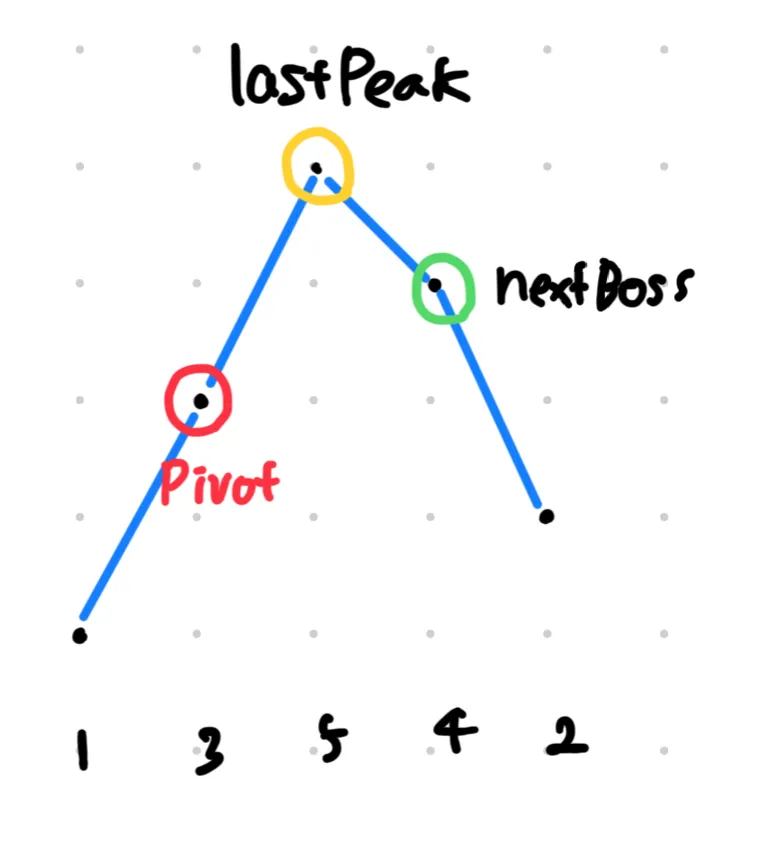
// 2. 새 지도자 찾아오기
int nextBoss = src.length - 1;
while(src[lastPeak - 1] >= src[nextBoss]) nextBoss--;
// 3. 지도자의 세대 교체
swap(src, lastPeak - 1, nextBoss);
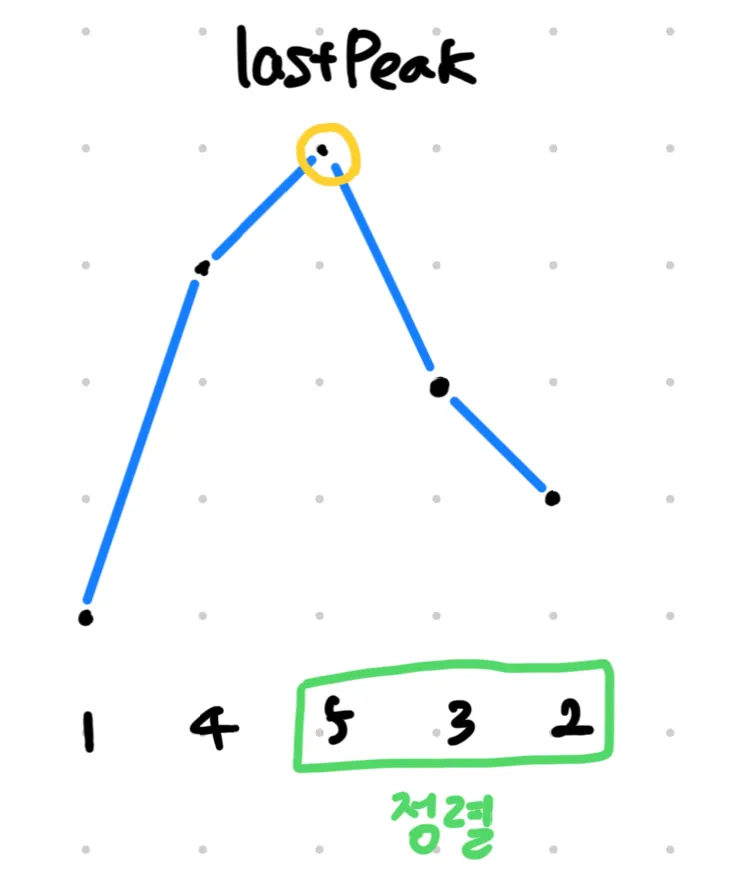
// 4. 새로운 조직의 시작 - 뒤 정렬
for(int left = lastPeak, right = src.length - 1; left < right; left++, right--) {
swap(src, left, right);
}
return true;
}
private static void swap(char[] src, int i, int j) {
char temp = src[i];
src[i] = src[j];
src[j] = temp;
}
static void permutationByNp() {
Arrays.sort(src);
do {
System.out.println(Arrays.toString(src));
} while (nextPermutation());
}
JavaScript
복사
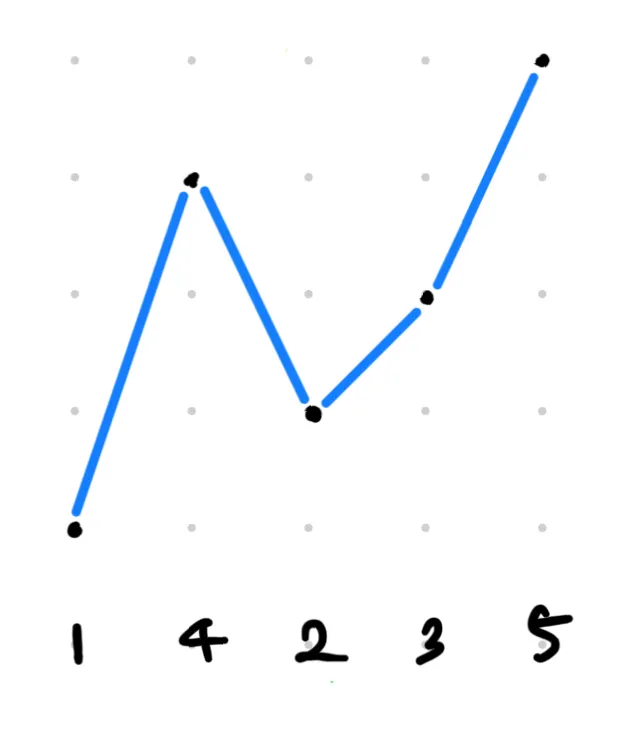
각 인덱스 값을 비교하여 모든 경우의 인덱스 값을 뽑는 방법
배열을 가장 작은 값으로 정렬한 뒤, 다음 큰 순열을 찾는 과정을 반복
1.
새로운 지도자 찾기
뒤에서부터 i < i + 1 를 만족하는 가장 높은 정점 lastPeak을 찾는다.
2.
뒤에서부터 lastPeak - 1 이후 요소 중 lastPeak - 1의 값보다 더 큰 값 nextBoss를 찾는다.
3.
lastPeak - 1의 값과 nextBoss값을 교환
4.
lastPeak에서부터 배열의 끝까지 오름차순으로 정렬
next permutation을 사용하여 조합도 구할 수 있음!
0과 1로 이루어진 원소로 구성 (선택해야하는 갯수만큼 1 넣기)